С операционной точки зрения, мы можем определить алгоритм, как конечную последовательность команд, использующих исходные данные для получения результата. С функциональной точки зрения это отображение $f: X \rightarrow Y$ , где $X$ - входные данные $Y$ - элемент результирующего множества.

О-нотация

Одну и ту же задачу зачастую можно решать большим количеством различных способов, сильно отличающихся друг от друга. Но как оценить это решение? Есть ли способ определить, лучше оно или хуже остальных и насколько?

Допустим, мы уже разработали некий АбстрактныйАлгоритм. Если мы его запустим, но можем узнать:

Насколько долго он работал(обозначим как $T$ )
Сколько памяти использовал(обозначим как $M$ )
и т.д.

Может показаться, что этого достаточно, но мы решили отправить АбстрактныйАлгоритм нашему АбстрактномуДругу, у которого компьютер намного хуже нашего. И оказалось, что то, что у нас занимало 1 минуту, у АбстрактногоДруга занимает 2 часа.

Мы хотим избежать подобных проблем. Поэтому решаем оценивать наш АбстрактныйАлгоритм не с секундомером, а по количеству операций(абстрактных).

Рассмотрим небольшую функцию из алгоритма.

Haskell:
exists :: [Int] -> Int -> Bool

exists (h:_tail) tgt = findElement _tail tgt $ (h == tgt) 
exists x target      = (x == tgt)

Python:
def exists(arr, tgt):
    for e in arr:
        if e == tgt:
            return True
    return False

Разбор примера и определения

Видим, что функция просто проверяет, есть ли элемент в массиве. Посчитаем, сколько операций для этого требуется(с учётом того, что размер нашего массива $n$ ):

В худшем случае $n$ операций для обхода массива( $for$ )
В худшем случае $n$ операций сравнения( $if$ )
Одна операция возврата результата( $return$ )

В сумме получили: $n + n + 1= 2n+1$ операций. Обратим внимание на фразу в худшем случае. Под этим мы подразумеваем, что количество операций может быть меньше, но, например, в случае, когда $tgt$ - последний, нам потребуется именно столько $(n)$ операций. Для удобства обозначают $O(n)$ . Для операции возврата значения нам всегда требуется одна операция(и в худшем и в лучшем случае). Для лучшего случая есть обозначение $\Omega(1)$ . А если $O(1)$ и $\Omega(1)$ , то $\Theta(1)$ .

Теперь обобщим результат из нашего пример. Получим: $O(n) + O(n) + \Theta(1)$ .

Заметим ещё одну деталь. Нам нужно знать, сколько операций требуется для вычисления не только на фиксированном размере массива, намного интереснее знать, как растёт сложность нашего алгоритма при росте $n$ (будем называть это число размером входа).

Выражение $O(n) + O(n) + \Theta(1)$ сейчас не является для нас чем-то удобным, так как мы не можем производить над ним какие-то операции. Для решения этой проблемы формализуем наши определения:

$O(n)$ : Пусть, начиная с некоторого размера входа $k$ сложность $f$ нашего алгоритма меньше или равна некоторой другой сложности $g$ , умноженной на какую-то константу $C$ . Тогда $f = O(g)$

Запишем это выражение ещё более формально: Пусть $f,g: R^+ \rightarrow R^+$ тогда $\exists C,k$ такие что $\forall l \geq k: f(l) \leq C * g(l) \Rightarrow f = O(g)$

$\Omega(n)$ : Пусть, начиная с некоторого размера входа $k$ сложность $f$ нашего алгоритма больше или равна некоторой другой сложности $g$ , умноженной на какую-то константу $C$ . Тогда $f = \Omega(g)$

$\Theta(n)$ : $f=O(g) \land f=\Omega(g) \Rightarrow f = \Theta(g)$

Из определения выходит, что:

$n = O(n^2)$
$n+1=O(n)$
$n = O(n^2) \Rightarrow n^2 = \Omega(n)$
$n=O(n) \land n=\Omega(n) \Rightarrow n = \Theta(n)$

Вернёмся к нашему выражению и упростим его: $O(n) + O(n) + \Theta(1)=O(n)+O(n)+O(C)=O(n)$ То есть теперь мы можем сказать, что АбстрактныйАлгоритм выполняется за линейное время или $O(n)$

Резюмируем

На данный момент мы можем написать некоторый АбстрактныйАлгоритм, измерить его сложность при помощи $O,\Omega$ и $\Theta$ , а потом отправить АбстрактномуДругу и быть уверенным, что у него всё будет работать также хорошо, как и у вас.

Мастер-теорема

Мы уже умеем измерять сложности. Но что делать, если алгоритм рекурсивный? Мы ведь не можем так просто посчитать все возможные операции? Или всё-таки можем...

Немного изменим наш пример:

Haskell:
split :: [a] -> ([a], [a])
split l = splitAt (((length l) + 1) `div` 2) l

exists :: [Int] -> Int -> Bool
exists [x] tgt = x == tgt
exists arr tgt = uncurry (\x y -> (exists x tgt) || (exists y tgt)) (split arr)

Python:
import math

def exists(arr, tgt):
    length = len(arr)
    if length == 1:
        return arr[0] == tgt
    sep_id = math.ceil(length/2)
    return exists(arr[:sep_id],tgt) or exists(arr[sep_id:],tgt)

Теперь мы рекурсивно ищем элемент в правом и левом поддереве, пока длина массива не будет равна 1.

Рассмотрим часть соответствующего дерева рекурсивных вызовов.

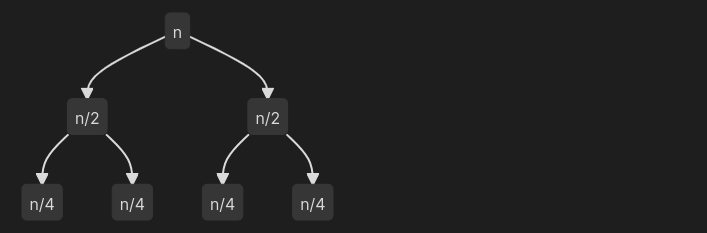
Видим, что размер входа на каждом последующем уровне становится в 2 раза меньше. Получается, что на $i$ уровне(с нуля) размер входа для одного вызова будет равен: $\frac{n}{2^i}$ При этом сложность суммарно на уровне будет: $2^i C$ А количество уровней будет равно $log_2(n)$ , т.е для $n=8$ - 3 уровня, для $n=16$ - 4 уровня и т.д.

Для того, чтобы найти общую сложность алгоритма, просуммируем по всем уровням: $T(n) = \sum_{i=0}^{log_2(n)} 2^i C = 2^{log_2(n)}C = O(n)$

Отсюда получается, что наш рекурсивный алгоритм также эффективен, как и его нерекурсивный аналог из предыдущего раздела.

Теперь, используя похожие умозаключения, сформулируем теорему, которая позволит оценить не только эту, но и многие другие рекурсивные задачи.

Теорема:

$\begin{equation*} \begin{cases} T(n) = O(1),n=1(1)\\ T(n) = a * T(\frac{n}{b}) + O(n^{c}), \ n > 1 \ (2)\end{cases} \end{equation*}$

,где $a$ - кол-во подзадач, $\frac{n}{b}$ - размер подзадачи, $O(n^c)$ - нерекурсивная сложность(сравнения, присваивания и т.д.)

Док-во: Как и в примере выше найдём суммарную сложность для всех уровней. Сложность одного вызова: $(\frac{n}{b^i})^c$ Сложность суммарно на уровне: $a^i(\frac{n}{b^i})^c$ Суммарная сложность: $\sum^{log_b(n)}_{i=0} a^i (\frac{n}{b^i})^c$

Подставим получившийся результат в выражение $(2)$ системы:

$T(n) = a * T(\frac{n}{b}) + O(n^{c}) = \sum^{log_b(n)}_{i=0} a^i (\frac{n}{b^i})^c + O(1)=$

$n^c \sum^{log_b(n)}_{i=0} (\frac{a}{b^{c}})^i + O(1)$

Результат полученного выражения зависит только от $\frac{a}{b^{c}}$ : $\frac{a}{b^{c}} = 1 \Leftrightarrow a = b^{c} \Leftrightarrow log_b(a) = c$ Получаем всего 3 случая:

$log_b(a) = c$ : $n^c \sum_{i=0}^{lob_b(n)} (\frac{a}{b^{c}})^i + O(1) = n^c \sum_{i=0}^{lob_b(n)} (\frac{a}{b^{log_b(a)}})^i + O(1) = n^c \sum_{i=0}^{lob_b(n)} 1^i + O(1) = n^c(log_b(n) + 1) + O(1) =$ $O(n^c \ log_b(n))$
$log_b(a) < c$ : $n^c \sum_{i=0}^{lob_b(n)} (\frac{a}{b^{c}})^i + O(1) = O(n^c)$
$log_b(a) > c$ : $n^c \sum_{i=0}^{lob_b(n)} (\frac{a}{b^{c}})^i + O(1) = O(n^c (\frac{a}{b^{c}})^{log_b(n)}) = O(n^c \frac{a^{log_b(n)}}{b^{log_bn \ c}}) = O(n^c \frac{a^{log_b(n)}}{n^c}) = O(a^{log_b(n)})$

Резюмируем

Для рекурсивной подзадачи вида: $\begin{equation*} \begin{cases} T(n) = O(1),\ n=1 \ \\ T(n) = a * T(\frac{n}{b}) + O(n^{c}), \ n > 1 \ \end{cases} \end{equation*}$ Сложность будет равна:

$log_b(a) = c \Rightarrow O(n^c \ log_b(n))$
$log_b(a) < c \Rightarrow O(n^c)$
$log_b(a) > c \Rightarrow O(a^{log_b(n)})$

Вернёмся к нашему примеру и оценим его с помощью теоремы:

$T(n) = 2 * T(\frac{n}{2}) + O(n^{0})$ Т.к. $log_2(2) > 0$ , то $T(n) = O(2^{log_2(n)}) = O(n)$ , что подтверждает нашу оценку выше.